Des interactions simples aux évolutions riches
Introduction
Le Jeu de la Vie, conçu par le mathématicien britannique John Horton Conway, est un automate cellulaire fascinant. À partir de règles simples, il permet d’observer des comportements émergents complexes. Cet article explore les principes de base du Jeu de la Vie, présente des exemples en deux et trois dimensions, et met en lumière les parallèles avec les graphes complexes, un domaine de recherche clé pour comprendre les dynamiques dans des réseaux variés.
Les règles du Jeu de la Vie
Le Jeu de la Vie se déroule sur une grille de cellules, où chaque cellule peut être vivante ou morte. Les règles d’évolution, simples mais puissantes, déterminent l’état futur des cellules en fonction de leurs voisins immédiats :
Naissance
Une cellule morte devient vivante si elle a exactement trois cellules vivantes autour d’elle.

Survie
Une cellule vivante reste vivante si elle a deux ou trois cellules vivantes autour d’elle.

Mort
Dans tous les autres cas, une cellule vivante meurt (solitude ou surpopulation).

Les motifs évolués
Le Jeu de la Vie a permis de découvrir une variété de motifs fascinants, classés en plusieurs catégories :
Motifs stables
Ces configurations restent inchangées au fil des générations, comme le bloc ou le bateau.

Oscillateurs
Ces motifs reviennent à leur état initial après un certain nombre de générations, tels que le clignoteur ou le crapaud.

Vaisseaux spatiaux
Ces configurations se déplacent dans la grille, le plus célèbre étant le planeur qui traverse l’écran.

Jeu de la Vie et modèle de Turing
Une des découvertes majeures est que le Jeu de la Vie est une machine de Turing universelle. Cela signifie qu’il peut simuler n’importe quel calcul logique ou algorithme, prouvant sa capacité à effectuer des calculs complexes à partir de règles simples. Cette compatibilité avec le modèle de Turing ouvre des perspectives intéressantes sur l’étude des systèmes dynamiques et des automates cellulaires.
Exemples 2D et 3D
En utilisant le code JavaScript, nous pouvons simuler le Jeu de la Vie sur une grille bidimensionnelle ou tridimensionnelle en changeant un peu des règles. Les boutons oranges placés sous les vidéos vous permettent de tester les différents modèles, et de les relancer car le placement initial est aléatoire. Attention, les démonstrations en 3D demandent une configuration puissante : une bonne carte graphique est requise !
Conway 2D
Voici une version classique du jeu de la vie, mais avec des côtés qui correspondent, c’est à dire qu’un planeur peut franchir une bordure pour ressortir sur le côté opposé.
Conway 2D perspective
Cette version reprend la précédente, avec des états supplémentaires pour indiquer les zones qui n’ont pas été modifiées. Le script est à tester sous la vidéo.
Conway 3D
Pour passer en 3D, on modifie les lois de Conway car on peut considérer qu’il y a 24 voisins autour de chaque cellule.
Conway 3D
En fonction des paramètres, on obtient des colonies de cellules évanescentes ou au contraire des envahissement de l’espace.
Conway 3D
L’équilibre en 3D est beaucoup plus compliqué à trouver, entre les naissances et les morts des cellules.
Conway 3D
Les conditions initiales jouent un rôle plus important en 3D. En 2D, la population se régule rapidement.
Conway 3D
Comme pour le script 2D, le script 3D fait correspondre les faces opposées du cube.
Conway 3D
Les algorithmes permettent également de distinguer plusieurs générations de cellules.
Conway 3D
La version 3D montre moins les déplacements, mais propose plusieurs sortes de croissance des cellules.
Conway 3D
En 3D, on peut retrouver des « blinker » mais les « glider » et les formes évoluées de motifs sont rares.
Conway 3D
Pour retrouver des motifs animées, mieux vaut appliquer les règles 2D sur les plans (xy), (xz) et (yz).
Similitudes avec les graphes complexes
Les graphes complexes, constitués de sommets et d’arêtes, sont utilisés pour modéliser une multitude de systèmes réels, des réseaux sociaux aux réseaux biologiques. Comme le Jeu de la Vie, les interactions simples dans ces graphes peuvent mener à des comportements émergents complexes :
Interactions simples
Dans les deux cas, des règles locales (voisinage) déterminent l’évolution du système.
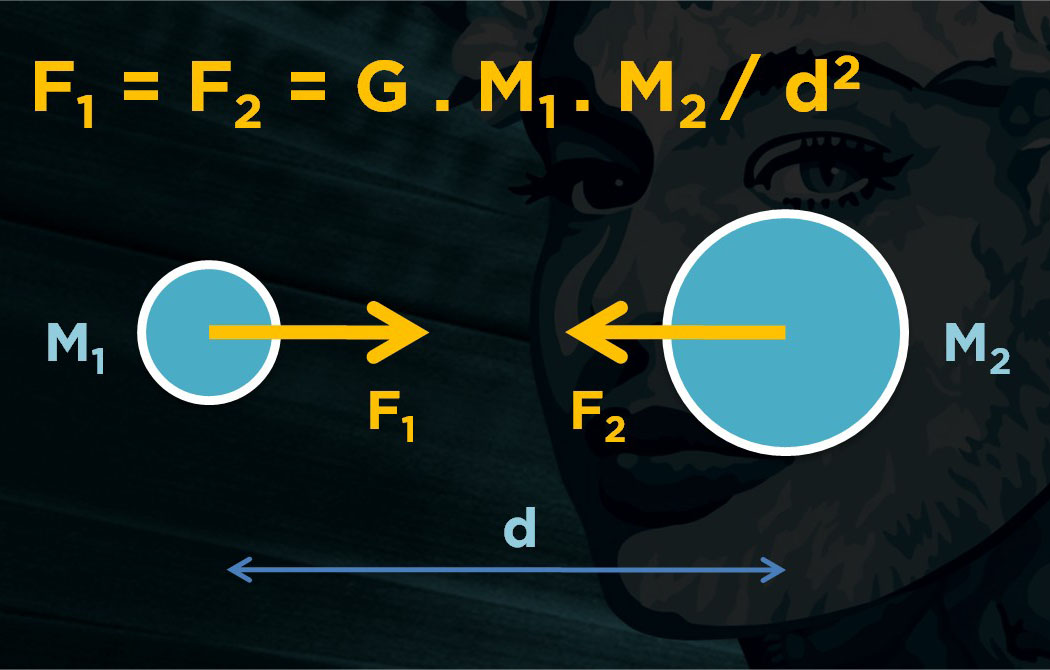
Les lois de Newton et leurs dérivées sont des interactions simples, qui servent à modéliser des liens lorsque l’on trace un graphe complexe. Des données liées vont s’attirer comme des planètes, avec une force de répulsion en plus, pour éviter les collisions et améliorer la lisibilité des cartes.
Évolutions complexes
Des structures émergent de manière imprévisible, illustrant la richesse dynamique des deux modèles.
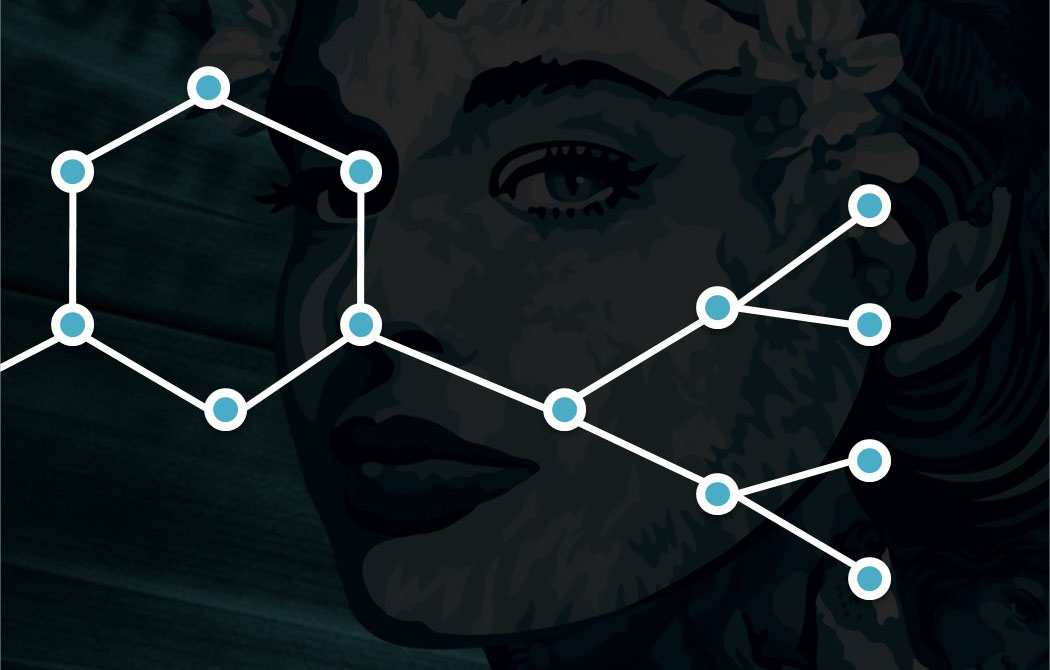
Des ces interactions simples, attractions et répulsions, naissent des organisations régulières et structurées, qui combiennt des boucles, des arbres, et des chemins. Cette répartition intelligente des données utilise les mêmes équations que l’apprentissage en I.A..
Par exemple, la propagation d’une information dans un réseau social peut être comparée à la propagation d’un motif dans le Jeu de la Vie. Dans les deux cas, des interactions locales engendrent des dynamiques globales complexes.