From Simple Interactions to Rich Evolutions
Introduction
Conway’s Game of Life, created by British mathematician John Horton Conway, is a fascinating cellular automaton. It demonstrates how complex emergent behaviors can arise from simple rules. This article explores the basic principles of the Game of Life, presents examples in two and three dimensions, and highlights parallels with complex graphs, a key research area for understanding dynamics in various networks.
The Rules of the Game of Life
The Game of Life takes place on a grid of cells, where each cell can be either alive or dead. The simple yet powerful evolution rules determine the future state of cells based on their immediate neighbors:
Birth
A dead cell becomes alive if it has exactly three living neighbors.

Survival
A living cell remains alive if it has two or three living neighbors.

Death
In all other cases, a living cell dies (due to isolation or overpopulation).

Evolved Patterns
The Game of Life has revealed a variety of fascinating patterns, categorized into several types:
Stable Patterns
These configurations remain unchanged over generations, such as the block or the boat.

Oscillators
These patterns return to their initial state after a certain number of generations, like the blinker or the toad.

Spaceships
These configurations move across the grid, the most famous being the glider that traverses the screen.

Game of Life and Turing Model
One of the major discoveries is that the Game of Life is a universal Turing machine. This means it can simulate any logical calculation or algorithm, proving its capacity to perform complex computations from simple rules. This compatibility with the Turing model opens interesting perspectives for studying dynamic systems and cellular automata.
2D and 3D Examples
Using JavaScript code, we can simulate the Game of Life on a two-dimensional or three-dimensional grid by slightly changing the rules. The orange buttons below the videos allow you to test different models and restart them since the initial placement is random. Note that 3D demonstrations require a powerful configuration: a good graphics card is necessary!
Conway 2D
Here is a classic version of the Game of Life, but with wrapping edges, meaning a glider can cross one border and reappear on the opposite side.
Conway 2D Perspective
This version builds on the previous one, with additional states to indicate areas that have not changed. Test the script below the video.
Conway 3D
To transition to 3D, we modify Conway’s rules as there are 24 neighbors around each cell.
Conway 3D
Depending on the parameters, we get either ephemeral cell colonies or space invasions.
Conway 3D
Finding equilibrium in 3D is much more complex, balancing cell births and deaths.
Conway 3D
Initial conditions play a more significant role in 3D. In 2D, the population quickly stabilizes.
Conway 3D
Like the 2D script, the 3D script wraps the cube’s opposite faces.
Conway 3D
The algorithms can also distinguish several generations of cells.
Conway 3D
The 3D version shows fewer movements but offers various types of cell growth.
Conway 3D
In 3D, we can find “blinkers” but “gliders” and advanced patterns are rare.
Conway 3D
To find animated patterns, it is better to apply 2D rules on the (xy), (xz), and (yz) planes.
Similarities with Complex Graphs
Complex graphs, consisting of nodes and edges, are used to model a multitude of real systems, from social networks to biological networks. Like the Game of Life, simple interactions in these graphs can lead to complex emergent behaviors:
Simple Interactions
In both cases, local rules (neighborhood) determine the system’s evolution.
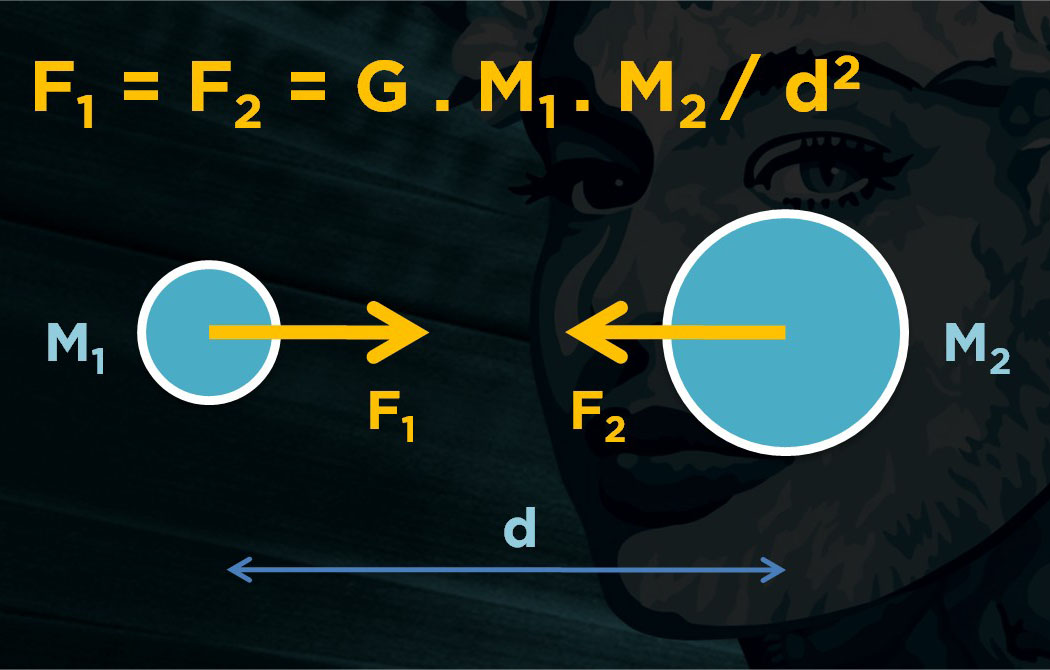
Newton’s laws and their derivatives are simple interactions used to model connections when plotting a complex graph. Related data attract each other like planets, with an added repulsive force to avoid collisions and improve map readability.
Complex Evolutions
Structures emerge unpredictably, illustrating the dynamic richness of both models.
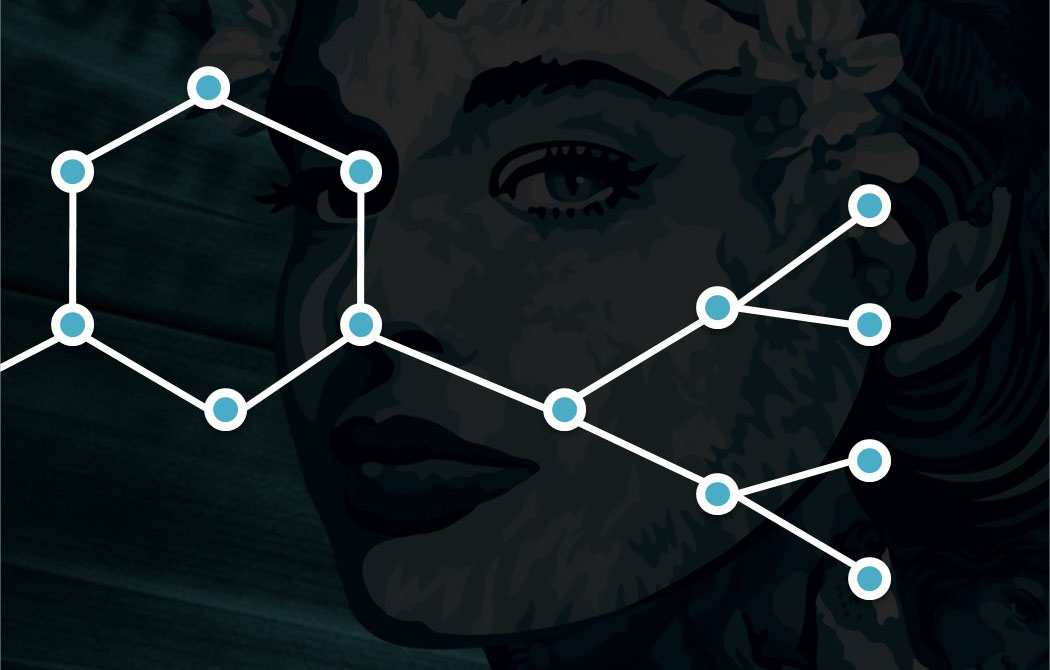
From these simple interactions, attractions, and repulsions, arise regular and structured organizations combining loops, trees, and paths. This intelligent data distribution uses the same equations as AI learning.
For example, the propagation of information in a social network can be compared to the propagation of a pattern in the Game of Life. In both cases, local interactions lead to complex global dynamics.